DiceCTF 2022 @Hope Writeup

DiceCTF @Hope is a nice competition, I worked with Frankss and Monad to solve the challenges. Our final rank is #21.

Categories	Solved	Writeup
crypto	6/8	jump
misc	5/8	TBA
pwn	3/5	TBA
rev	5/11	TBA
web	7/10	TBA

Crypto

obp

The unbreakable One Byte Pad

by BrownieInMotion

The given python script uses One Time Pad to encrypt the message. However, the perfectly security of the OTP only happens when the length of the key is as the same as the plaintext.

import random

with open('flag.txt', 'rb') as f:
    plaintext = f.read()

key = random.randrange(256)
ciphertext = [key ^ byte for byte in plaintext]

with open('output.txt', 'w') as f:
    f.write(bytes(ciphertext).hex())

In this scenario, using only one byte key can be decrypted with brute force in possibility polynomial time (PPT). I used Cyberchef for xor brute force.

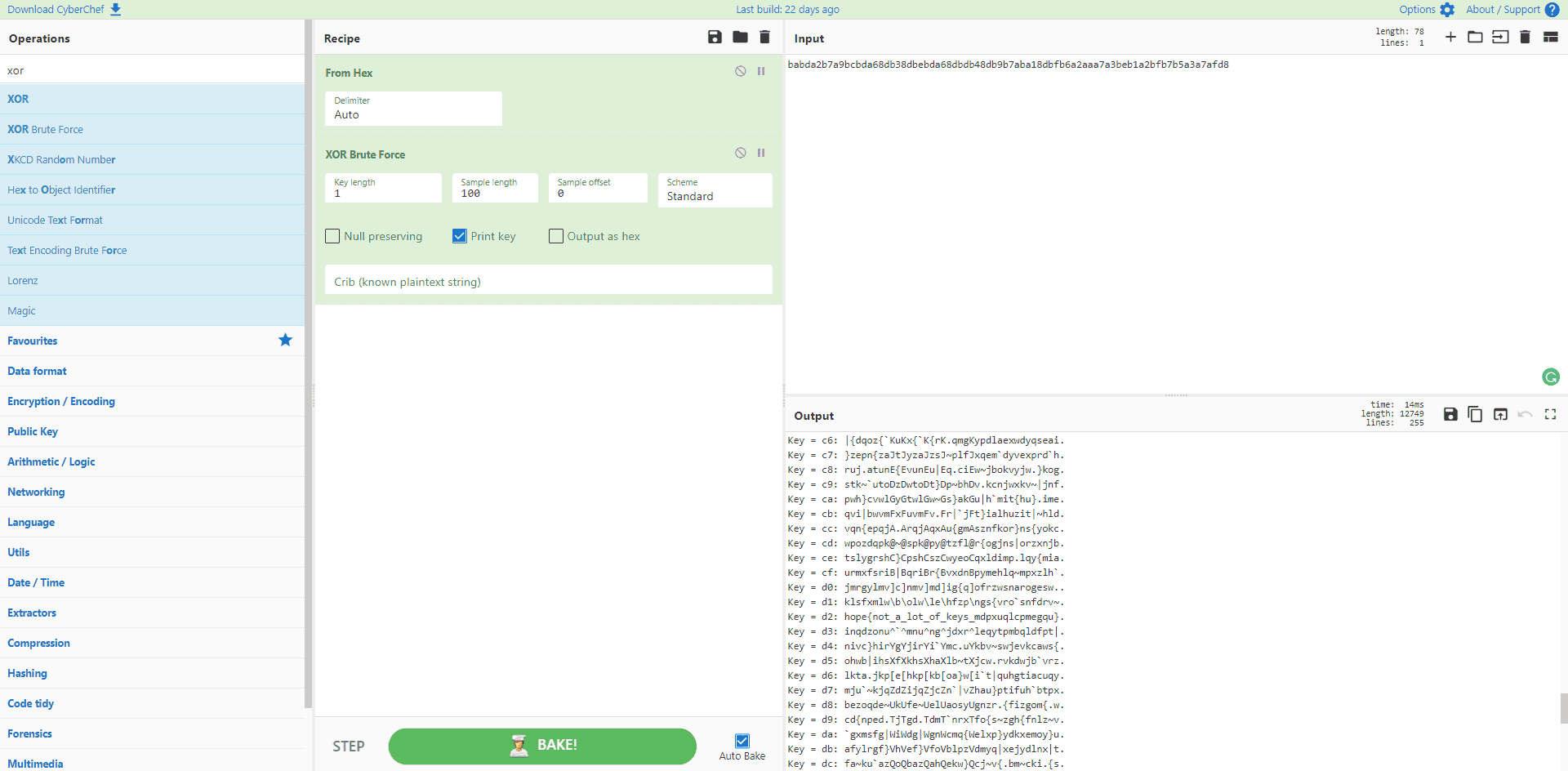
The correct key is 0xd2.

pem

PEM stands for Prime Encryption Method, I think.

by ireland

The given python code accidently output the private key instead of the public key. We can use PKCS1_OAEP decrypt by loading the given private key.

from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP

with open('flag.txt','rb') as f:
    flag = f.read()

key = RSA.generate(2048)
cipher_rsa = PKCS1_OAEP.new(key)
enc = cipher_rsa.encrypt(flag)

with open('privatekey.pem','wb') as f:
    f.write(key.export_key('PEM'))

with open("encrypted.bin", "wb") as f:
    f.write(enc)

The payload as follow:

>>> from Crypto.Cipher import PKCS1_OAEP
>>> from Crypto.PublicKey import RSA
>>> ciphertext = open('encrypted.bin', 'rb').read()
>>> key = RSA.importKey(open('privatekey.pem').read())
>>> cipher = PKCS1_OAEP.new(key)
>>> print(cipher.decrypt(ciphertext))
b'hope{crypto_more_like_rtfm_f280d8e}'

kfb

if keys make stuff secure then why don't we use them more

nc mc.ax 31968

by kfb

The given python code reads the flag file, and encrypted it with AES ECB mode with a key length of 16 bytes.

#!/usr/local/bin/python -u

from Crypto.Cipher import AES
from Crypto.Random import get_random_bytes
from Crypto.Util.Padding import pad
from Crypto.Util.strxor import strxor
from more_itertools import ichunked

BLOCK = AES.block_size
FLAG = open('flag.txt', 'rb').read().strip()

def encrypt_block(k, pt):
  cipher = AES.new(k, AES.MODE_ECB)
  return cipher.encrypt(pt)

def encrypt(k, pt):
  assert len(k) == BLOCK
  pt = pad(pt, BLOCK)
  ct = b''
  for bk in ichunked(pt, BLOCK):
    ct += strxor(encrypt_block(k, k), bytes(bk))
  return ct

def main():
  k = get_random_bytes(BLOCK)
  enc = encrypt(k, FLAG)
  print(f'> {enc.hex()}')

  pt = bytes.fromhex(input('< '))[:BLOCK]
  enc = encrypt(k, pt)
  print(f'> {enc.hex()}')

if __name__ == '__main__':
  main()

The same key is then used to encrypt a user given hex message, the maximum length of this message is 32 bytes.

The solution is simple: gives an all 0s message, the encrypted ciphertext is as the same as the key, as the ECB mode simply xor the key and the message blocks. Here's an external link for ECB mode: Wikipedia ECB Mode.

For example, the server gives me ciphertext cb98a2eab4b86597f93a1e046bfd88e2d083bbeca48c779af93a021e78f7b3d5c6a8b9e1a0a470aac47a455e26f58e8ac6cfeabcaab736c1db4e71 6c1996ebba. I divided them into 4 blocks, 16 bytes (32 hex characters) per block:

cb98a2eab4b86597f93a1e046bfd88e2
d083bbeca48c779af93a021e78f7b3d5
c6a8b9e1a0a470aac47a455e26f58e8a
c6cfeabcaab736c1db4e716c1996ebba

Then padding 0s into server, the response (key) is a3f7d28fcfd303f5a649766b1e91ecbdb3e7c29fdfc313e5b659667b0e81fcad. Use this key for each block, find the flag:

hope{kfb_should_
stick_to_stuff_h
e_knows_b3358db7
e883ed54}.......

DESpicable you

I've told my minions to brew up a new type of block cipher! (written in python 2.7)

by greenbeans

The given python code seems to be secure. It generates random key, and encrypt the message with 8 byte block.

The first problem is the rekey function. If you test this function, you would find out that the key doesn't change after the rekey. The string in python is passed to the function with only value instead of address, change the value in rekey for key doesn't affect the caller's key.

from os import urandom

def encipher(a,b):
    c = ''
    for i, j in zip(a,b):
        c+=chr(ord(i)^ord(j))
    return c

def rekey(key):
    k = ""
    for i,c in enumerate(key):
        if i == len(key)-1:
            k += c
            k += chr(ord(c)^ord(key[0]))
        else:
            k += c
            k += chr(ord(c)^ord(key[i+1]))
    key = k

def main():
    key = urandom(8)

    with open('flag.txt') as f:
        plaintext = f.read()

    i = 0
    ct = ''
    while i < len(plaintext):
        ct += encipher(plaintext[i:i+len(key)],key)
        i += len(key)
        rekey(key)
    f2 = open('output.txt', 'w')
    f2.write(ct)
    f2.close()

main()

The second problem is the prefix of the plaintext, we already known, is the hope{'. Using this plaintext, we can find out the first 5 bytes of the key is 88 15 03 8d 50.

Another knowledge we have is the characters in the plaintext should be all printable characters. Thus, we brute force the every 6th/7th/8th byte in blocks. The only valid case is that the xor result gives only printable characters.

Only the 5th byte has multiple possible key values. But with some practice, we can find the last 3 bytes of the key are 6e c1 61.

The final flag is: hope{maybe_1_sh0ulD_h4v3_h1R3d_4_5p3c1471st_5tgkjs3bgRh}.

replacement

Oh no, my light reading got all mixed up!

by BrownieInMotion

Cipher python code is very simple, only shuffles all the characters in the plaintext.

import random

with open('text.txt') as f:
    plaintext = f.read()

with open('flag.txt') as f:
    plaintext += '\n' + f.read()

characters = set(plaintext) - {'\n'}

shuffled = list(characters)
random.shuffle(shuffled)

replacement = dict(zip(characters, shuffled))

ciphertext = ''.join(replacement.get(c, c) for c in plaintext)

with open('output.txt', 'w') as f:
    f.write(ciphertext)

Notice that blanks are shuffled as well. Luckily, the new liners are stayed the same. We can have the following ciphertext:

oiqsygh"dg"g}y__"Mygkwg_ySdB
bxgh"Vyg"g}y__"Mygkwg_ySdbrg_hyg"SSwlSsydgwVy.gkhygfljiqsgsh"SSyi_BgnVyrg hwg"i "t_gf"qdgy,sy__qVyg"kkySkqwSgkwgyVy.tkhqSMgoiqsyg_"qdrgkhwlMhkgkh"kgkhq_g_wlSdydgqSky.y_kqSMrg"Sdg.y_wiVydgkwg.y"dgkhyg}y__"MyB
bxg_h"iig_ySdgqkgkwgawjgqSgkhyg}w_kgswSVwilkydg "tgfw__qjiyrbgy,fwlSdydgoiqsygcl.khy.rgbl_qSMg"g}q,kl.ygwcgf.qV"kyg"Sdgfljiqsgsh"SSyi_g"_g yiig"_gEytgqScw.}"kqwSg_ySkgjtgk.l_kydgswl.qy.b
nVygcwlSdgkhq_gk"iEgwcgy,syfkqwS"igsw}fiqs"kqwSgy,k.y}yitgqSk.qMlqSMBgvy"S hqiyrgawjgMwkghq}_yicg"g_"Sd qshB
bxkg_h"iigjyg"My_gtykgjycw.ygoiqsyg_ySd_g}yghy.g}y__"Myrgcw.g_hyg}l_kgySswdygqkgqSgkhyg}w_kgswSVwilkydg "tgfw__qjiyBgxSg"ddqkqwSrgqkgq_giq"jiygkwgjygdliigkwg.y"dgyVySgwSsygdysqfhy.ydbgkhwlMhkgawjBgbmyswSditrgdysqfhy.qSMgqkgq_gMwqSMgkwgjyg"ghy"d"shyBbg{hy.ycw.ygawjg}"dyghq}_yicg"gslfgwcgky"gkwgMwg qkhghq_g_"Sd qshB

Oq"g"gsw}fiy,g_y.qy_gwcgdq_Mlq_y_g"Sdgkhygl_ygwcgsiyVy.gkyshSwiwMtgkwg_"}fiygqScw.}"kqwSgc.w}g"iiyMyditg_ysl.ygsh"SSyi_rgnVyg.yswVy.ydg"gc."skqwSgwcgkhyg}y__"Myg"SdgwcgkhygEytBgatg"ffitqSMg"iigwcghy.gswS_qdy."jiygqSkyiiqMySsyg"Sdg"ghqdywl_gel"Skqktgwcgsw}flk"kqwS"igfw y.rg_hyg "_g"jiygkwg.yswVy.gkhygfi"qSky,krg.yswdyg"g}y__"Myg"Sdgf"__gqkgwSgkwgawjg"_gqcgSwkhqSMgh"dgh"ffySydBgpSitgkhySgdqdg_hyg"skl"iitg.y"dgkhygfi"qSky,kB

hwfyASwkTkhyTM.y"ky_kT_ qkshy.wwTqjf_S,tjEyS"i,}cSdIccd_u

Using brute force is unacceptable. However, we can take it a bite from the new liners. We can have the first guess:

• Almost all the previous character from the new liners are . (dots).

With this assumption, we can quickly jump to the second:

• Almost all the dots should be followed with a (blank).

Then, starts from the blanks, we have another assumption:

• Almost all the blanks should after some punctuations like , (commas).

Now, we guess the last line should be flag. We can guess:

• In the most scenarios, only the flag can contain _ (underlines), {} (open and close braces).

Now, we already have enough information to run a A*-like search in substitution cipher. We can decrypt most of the characters in an ignored-case search. The only problem is some special characters:

• " (quotations): should be presents in the beginning of a word or after/before a punctuation. Otherwise, in the end of a line.
• Alice, Bob, Eve: special names in the cryptography, should be useful for alphabet character replacements.
• Uppercase alphabets: only shows a few times, shouldn't be a problem.

OK, now we have mostly ciphertext decrypted. However, the flag is not correct. What's the key point? The problem is the special character only presents once in the flag, this is the last cipher replacement. Find the last and the only reflection we haven't used: I -> j.

Finally, we find the plaintext:

Alice had a message to send.
"I have a message to send", she announced over the public channels. Eve, who always paid excessive attention to everything Alice said, thought that this sounded interesting, and resolved to read the message.
"I shall send it to Bob in the most convoluted way possible," expounded Alice further, "using a mixture of private and public channels as well as key information sent by trusted courier"
Eve found this talk of exceptional complication extremely intriguing. Meanwhile, Bob got himself a sandwich.
"It shall be ages yet before Alice sends me her message, for she must encode it in the most convoluted way possible. In addition, it is liable to be dull to read even once deciphered" thought Bob. "Secondly, deciphering it is going to be a headache." Therefore Bob made himself a cup of tea to go with his sandwich.

Via a complex series of disguises and the use of clever technology to sample information from allegedly secure channels, Eve recovered a fraction of the message and of the key. By applying all of her considerable intelligence and a hideous quantity of computational power, she was able to recover the plaintext, recode a message and pass it on to Bob as if nothing had happened. Only then did she actually read the plaintext.

hope{not_the_greatest_switcheroo_ibpsnxybkenalxmfndjffds}

reverse-rsa

I'll tell you my flag if you can prove you already know it!

nc mc.ax 31669

by ireland

This is a static res public-private key generation problem. The python code only checks the flag format in the plaintext, maybe, in some practice, we can construct a key pair, to make the hope{.*} presents in the plaintext.

#!/usr/local/bin/python

import re
from Crypto.Util.number import isPrime, GCD

flag_regex = rb"hope{[a-zA-Z0-9_\-]+}"

with open("ciphertext.txt", "r") as f:
    c = int(f.read(), 10)

print(f"Welcome to reverse RSA! The encrypted flag is {c}.  Please provide the private key.")

p = int(input("p: "), 10)
q = int(input("q: "), 10)
e = int(input("e: "), 10)

N = p * q
phi = (p-1) * (q-1)

if (p < 3) or not isPrime(p) or (q < 3) or not isPrime(q) or (e < 2) or (e > phi) or GCD(p,q) > 1 or GCD(e, phi) != 1:
    print("Invalid private key")
    exit()


d = pow(e, -1, phi)
m = pow(c, d, N)

m = int.to_bytes(m, 256, 'little')
m = m.strip(b"\x00")

if re.fullmatch(flag_regex, m) is not None:
    print("Clearly, you must already know the flag!")

    with open('flag.txt','rb') as f:
        flag = f.read()
        print(flag.decode())

else:
    print("hack harder")

This post claims this problem: construct private / public keys.

Here's an example solution:

p = 18237507977115134399
q = 13539415005905881139
e = 201049869065984997914383873658228289079

We can find the flag finally: hope{successful_decryption_doesnt_mean_correct_decryption_0363f29466b883edd763dc311716194d37dff5cd93cd4f1b4ac46152f4f9}